LeetCode（一）

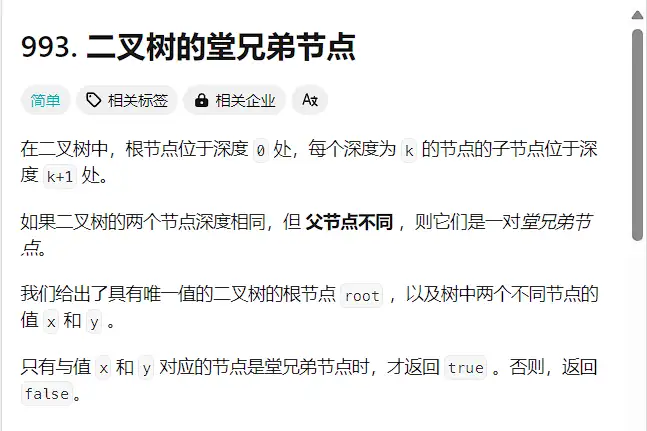
1.（993）【简单】二叉树的堂兄弟节点

解释

遍历二叉树以找到值为 x 和 y 的节点，同时记录它们的深度和它们父节点的信息。遍历可以使用深度优先搜索（DFS）或广度优先搜索（BFS）完成。以下是使用深度优先搜索（DFS）的方法：

1. 从根节点开始遍历二叉树。
2. 对每个访问的节点，记录其子节点的值、深度和父节点。
3. 当找到值为 x 或 y 的节点时，记录该节点的深度和父节点。
4. 完成遍历后，比较值为 x 和 y 的节点的深度和父节点信息：
   • 如果它们的深度相同但父节点不同，则返回 true。
   • 否则，返回 false。

代码

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def isCousins(self, root, x, y):
        """
        :type root: TreeNode
        :type x: int
        :type y: int
        :rtype: bool
        """
        depth = {}
        parent = {}

        def dfs(node, par=None, dep=0):
            if node:
                depth[node.val] = dep
                parent[node.val] = par
                dfs(node.left, node, dep + 1)
                dfs(node.right, node, dep + 1)
        
        dfs(root)
        return depth[x] == depth[y] and parent[x] != parent[y]
        

---

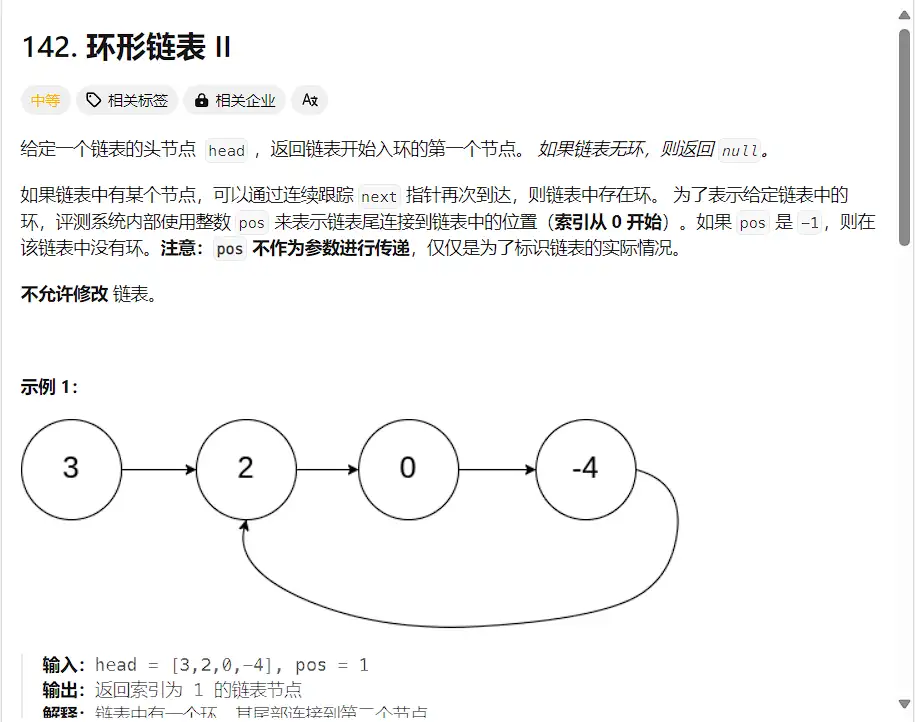
2.（920）【中等】环形链表

解释

快指针（fast） 2step
慢指针（slow） 1step
如果链表中有环--->这两个指针会相遇

假设从链表头到环的起点的距离为 a，环的起点到两指针相遇点的距离为 b，相遇点回到环的起点的距离为 c。

当慢指针进入环时，快指针已经在环内。为了让它们相遇，假设慢指针走了 b 的距离，快指针就走了 b+c 的距离，因为它的速度是慢指针的两倍。

所以我们有：

2(a+b) = a+b+c+b
a+b = c+b
a = c

这意味着从链表头到环的起点的距离等于从相遇点到环的起点的距离。

因此，当我们发现慢指针和快指针相遇时，我们可以将一个新的指针设置在链表的头部，并使其与慢指针以相同的速度移动。当这个新指针和慢指针相遇时，它们会在环的起点相遇。

代码

---

双指针

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def detectCycle(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        fast = head
        slow = head
        while fast and fast.next:
            fast = fast.next.next
            slow = slow.next
            if slow == fast:
                break
        if not fast or not fast.next:
            return None
        
        a = head
        while a != slow:
            a = a.next
            slow = slow.next
        return a

---

双指针优化

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def detectCycle(self, head):
        fast, slow = head, head
        while True:
            if not (fast and fast.next): return
            fast, slow = fast.next.next, slow.next
            if fast == slow: break
        fast = head
        while fast != slow:
            fast, slow = fast.next, slow.next
        return fast

---

双指针+哈希表

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def detectCycle(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        # 双指针+哈希表 双指针确定有环 然后哈希表寻找第一个进环的结点 时间复杂度 O(n) 空间复杂度 O(k) k指的是环中包含的结点个数
        # 结果：通过 用时和内存都不错 但是没有满足只使用O(1)的空间复杂度的要求
        # slow = fast = head
        # flag = 0
        # while fast and fast.next:
        #     if fast.next == slow or fast.next.next == slow:
        #         flag = 1
        #         break
        #     slow = slow.next
        #     fast = fast.next.next
        # if flag == 0:
        #     return
        # else:
        #     candidates = {}
        #     candidates[slow] = 1
        #     cur = slow.next
        #     while cur != slow:
        #         candidates[cur] = 1
        #         cur = cur.next
        #     cur = head
        #     while cur:
        #         if cur in candidates:
        #             return cur
        #         else:
        #             cur = cur.next

        # 直接使用哈希表 时间复杂度 O(n) 空间复杂度 O(n)
        # nodes = {}
        # cur = head
        # while cur:
        #     if cur not in nodes:
        #         nodes[cur] = 1
        #         cur = cur.next
        #     else:
        #         return cur
        # return

        # 只使用快慢指针 原因：假设从起点到环入口有a步 从环入口到快慢指针相遇点有b步 从相遇点到尾部有c步 那么慢指针一共走了a+b步 快指针一共走了a+b+n(b+c) 且a+b+n(b+c)=2(a+b) 可以得到a=c+(n-1)(b+c) 所以只需要再设置一个指针从head开始和slow一起一步一步移动 他们的相遇点就是环入口
        slow = fast = head
        flag = 0
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
            if fast == slow:
                flag = 1
                break
        if flag == 0:
            return
        else:
            ans = head
            while ans != slow:
                ans = ans.next
                slow = slow.next
            return ans

---